..

2024-07-17

最小環

• 任意兩點間的最短距離
• Floyd 算法為甚麼正確
• Floyd 算法求最小環
• 無負權的情況下求最小環

任意兩點間的最短距離

思考一個很經典的問題：給定一個簡單無向圖（有 $N$ 个結點 $1,2,3,\ldots, N$ 和 $M$ 條邊），如何求得任意起點 $s$ 到終點 $t$ 的最短距離？

「Floyd 算法。」遮似乎是個可以即答的問題。

我想，或許許多人同我一樣，在剛開始學習圖論的最短路算法時會被告知：

1. 若求解單源最短路，請使用 Dijkstra 算法；
2. 若要求任意兩點的最短路，請使用 Floyd 算法。

原因似乎出在複雜度。我們知道，使用堆優化的 Dijkstra 算法時間複雜度為 $O((N+M)\log{(N+M)})$¹，而 Floyd 算法為 $O(N^3)$。若执行 $N$ 次 Dijkstra 算法也祇需要 $O(N(N+M)\log{(N+M)})$ 的時間，稀疏圖情況下還是比 Floyd 算法優。那為甚麼我們似乎從不考慮 Dijkstra 算法呢，是因為一般遮種情況下邊都很多嗎？

說實話，我此前還真沒認真想過遮個問題。直到今年邀請賽前一晚在酒店睡前，康問了我遮個問題。我纔認真地想了遮件事。我想遮是一個很好的問題，很多時候，我們祇為了更快地「用」遮些方法去解決一些亟待處理的問題，反而忘了一些更深刻、本質的問題。

答案是 Floyd 算法還能處理邊權為負值的情況。

Floyd 算法為甚麼正確

要回答遮個問題，首先我們需要思考一下為甚麼 Floyd 算法是正確的。Floyd 算法是一個動態規劃算法，用狀態 $f(k, x, y)$ 表示由 $x$ 至 $y$ 僅通過 $\lbrace 1,2,3,\ldots,k\rbrace$ 的最短路。則答案為 $f(N, s, t)$，並有如下轉移：

\[f(k, x, y) = \min\lbrace f(k-1,x,y), f(k-1,x,k)+f(k-1,k,y) \rbrace.\]

即考慮當前情況下 $x,y$ 之間的最短路是否經過 $k$ 點進行轉移。一種編程的技巧名為「滾動數組」，因為每次轉移狀態 $k$ 祇與 $(k-1)$ 有關，所以可以祇用兩維來表示狀態，然後就得到常見的 Floyd 算法的寫法。知道遮一點，我們就可以理解為甚麼 「$k$」必須寫在循環的最外層。

由於 $f(k-1,x,y)$ 對應的最短路，除 $x,y$ 外是沒有 $k$ 的，而 $f(k-1,x,k)+f(k-1,k,y)$ 最多祇會經過一次 $k$，所以最短路上不會有兩個重复的結點，換言之，Floyd 算法求得的是路徑（path）。

Dijkstra 算法是無法處理負權邊的情況的，然而，當圖中存在負環，Floyd 算法還是能得到最小的路徑。

Floyd 算法求最小環

接著我們思考如何求簡單圖中的最小環。當然，我們希望求的是最小簡單環。我們發現，環上一定有一个編號最大的結點 $u$，这個貢獻可以在执行 Floyd 算法中考慮到：

\[\text{結點編號最大為 $u$ 的環的最小值}=\min_{x<u,y<u}\lbrace w(u,x) + f(u-1,x,y) + w(y,u) \rbrace,\]

其中，$w(v,u)$ 表示的是邊 $\lbrace v,u\rbrace$ 的權重。

無負權的情況下求最小環

我們再思考若圖中沒有負權邊，能否用 Dijkstra 算法計算最小環呢？

給定沒有負權的簡單無向圖 $G=(\mathcal{V},\mathcal{E})$，假設 $G$ 中存在最小環 $C$。考慮 $C$ 上的一個結點 $u$，首先可以證明對於 $C$ 上的任意一點 $x$，一定有 $u$ 到 $x$ 的最短路 $p(u,x)$ 落在 $C$ 上。

可以反證，假設 $p(u,x)$ 不在 $C$ 上。如果 $p(u,x)$ 除 $u, x$ 外與 $C$ 沒有交點，則可以在環 $C$ 上選擇一條 $u$ 至 $x$ 的路徑 $p^c(u,x)$，和 $p(u,x)$ 可以組成一個環，且該環長度會更小，矛盾。如果 $p(u,x)$ 除 $u,x$ 外與 $C$ 還有交點，那麼存在點 $v$，使得選擇 $p(u,x)$ 中 $u$ 到 $v$ 的路徑 $p(u,v)$ 與原來環上的 $p^c(u,v)$ 除 $u,v$ 外不相交，此時 $p^c(u,v)$ 和 $p(u,v)$ 組成一個更小的環，說明 $u$ 不在 $C$ 上，矛盾。

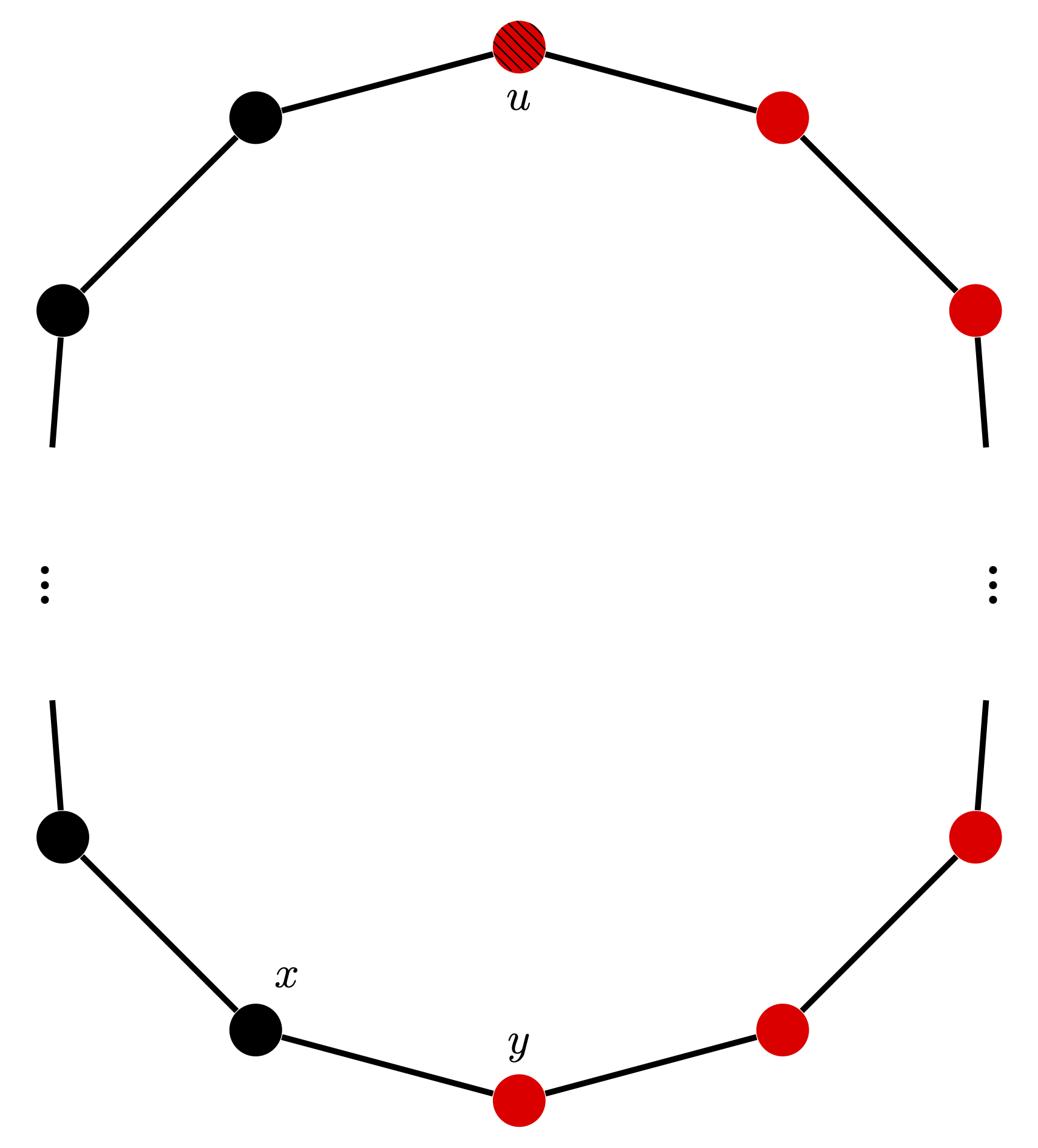
我們可以將環 $C$ 上的點排成一个圓，如下圖所示。由 $u$ 開始，逆時針依次考慮所有點 $x$，我們發現 $p(u,x)$ 一定落在 $x$ 的左邊（順時針方向）或右邊（逆時針方向），記左邊的路徑為 $p^l(u,x)$，右邊為 $p^r(u,x)$。 若 $p^l(u,x)\leq p^r(u,x)$，則將 $x$ 染為黑色，否則染為紅色，特別的，$u$ 既是黑色也是紅色。

很明顯，黑色和紅色點都是連續的。$u$ 既是紅色也是黑色，且環長至少為 $3$。那麼一定可以找到遮样的 $x,y\in C$，满足 $x$ 是黑色點，$y$ 是紅色點，且 $\lbrace x,y\rbrace\in\mathcal{E}(C)$。而此時，$p^l(u,x)=p(u,x),p^r(u,y)=p(u,y)$。遮說明我們可以在以 $u$ 為起點的單源最短路對應的生成樹 $T=(\mathcal{V}({T}),\mathcal{E}({T}))$²中找到 $x,y$，且需滿足 $\lbrace x,y\rbrace\notin \mathcal{E}({T})$。

於是可以通過 $N$ 次 Dijkstra 算法得到對應的 $N$ 棵生成樹，然後枚舉不在樹上的邊來計算最小環。時間複雜度為：$O(N(N+M)\log(N+M)+NM)$。

想了一下，發現遮樣還能求得一定經過給定點 $u$ 的最小環。需要用到求 LCA 的算法³，時间複雜度為：$O((N+M)\log(N+M)+M\log N)$。

---