..

2022-03-21

費馬原理與折射定律

首先思考這樣一個問題，這源於在前段時間進行的一場訓練：

假設在一個矩形稻田中，$A，B$ 分別在其左上角與右下角，並且在垂直方向距離 $A$ 點 $a$ 處有一水平分割線，此時一人欲從 $A$ 行至 $B$，但由於水平線上下方稻麥疏密不同導致他在上方行走速度爲 $v_1$ 而在下方行走速度爲 $v_2$。問其由 $A$ 行至 $B$ 花費最短時間為幾何。如下圖所示：

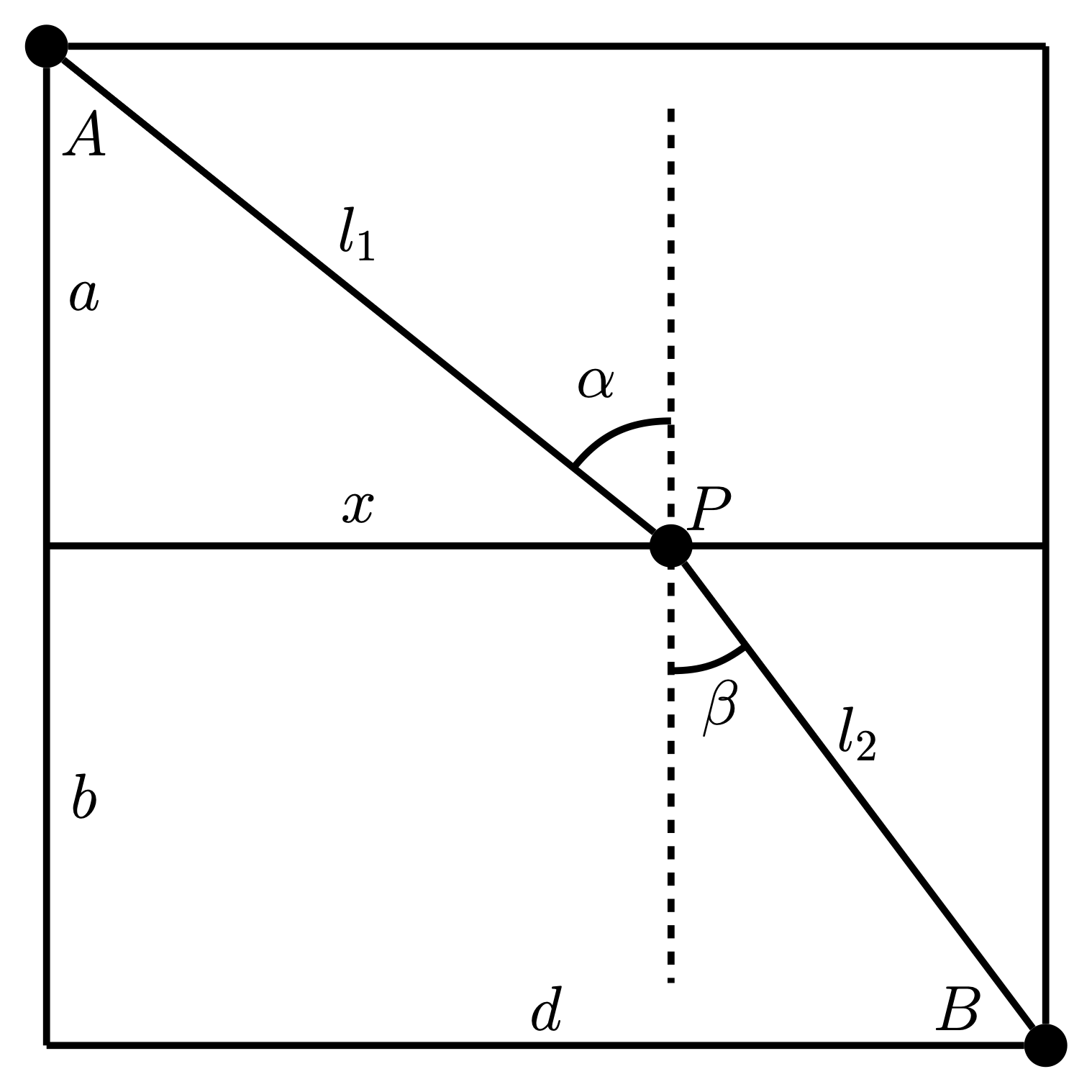
爲得到這個問題的解，可以設 $P$ 至 $a$ 所在垂直線的距離爲 $x$，那可得到時間代價爲：

\[t(x)=\frac{1}{v_1}\sqrt{x^2+a^2}+\frac{1}{v_2}\sqrt{(d-x)^2+b^2}\]

這顯然是一個關於 $x$ 的函數，於是進一步的對其求導得：

\[t'(x)=\frac{1}{v_1}\frac{x}{\sqrt{x^2+a^2}}-\frac{1}{v_2}\frac{d-x}{\sqrt{(d-x)^2+b^2}}\]

若進一步求導可以發現這是一個在 $(0,d)$ 單調增加的函數，並且由於 $t’(0)<0$ 且 $t’(d)>0$ 可知 $t’(x)$ 在 $(0,d)$ 上存在唯一零點 $x_0$。但若單純令 $t’(x)=0$ 將會發現問題會變爲求解一個四次方程。但注意到：

\[\frac{x}{\sqrt{x^2+a^2}}=\sin{\alpha},\frac{d-x}{\sqrt{(d-x)^2+b^2}}=\sin{\beta}\]

所以最优解將滿足條件：

\[\frac{\sin{\alpha}}{\sin{\beta}}=\frac{v_1}{v_2}\]

我們驚奇地發現，這其實就是折射定律（Snell’s Law）。而這樣證朙的思路其實是費馬原理：

Fermat’s principle states that the path taken by a ray between two given points is the path that can be traveled in the least time. ¹

費馬原理表朙了光線在兩點之間傳播采用最短時間的路線。

於是這個問題可以通過二分的方法解決，當然讀者會問，爲何要利用這個結論進行二分？直接二分 $x$ 不也很好？在此處確實如此，但當時遇到的問題稍微困難一些，矩形中有兩條水平線，此時若通过三分套二分的思路將會在評測中獲得 TLE 的好結果，正確做法應當是二分最初的”入射角”，通过 Snell’s Law 判斷是否會 “射” 到 $B$ 上，那就可在一个 $\log$ 下解決。

---